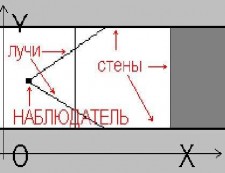
Реализуем все это следующим образом. Проверим на пересечение с лучом сначала вертикальные, а потом горизонтальные стены. Далее выберем ближайшее пересечение.

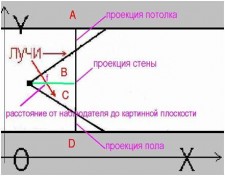
Пусть наблюдатель находиться в точке с координатами (x*,y*), а угол между лучом

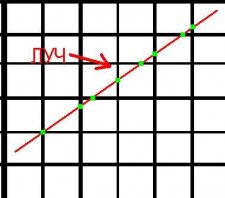
и положительным направлением оси 0X равен alpha. Будем считать, что клетка, содержащая игрока, имеет индекс (i*,j*), а шаг сетки равен h. Найдем точки пересечения луча с вертикальными линиями x=ih. Если направляющий вектор луча имеет положительную х-составляющую (cos(alpha)>0 => alpha от -pi/2 до pi/2), то ближайшая точка будет иметь координаты x1=(i*+1)h, y1=y*+(h-(x*-i*h))tan(alpha)=y*+(x1-x*)tan(alpha). При этом эта точка лежит на границе клетки (i*+1,[y1/h]). Если эта клетка занята стеной, то пересечение сразу получается в точке (x1,y1). При этом расстояние до точки пересечения будет равно d=(x1-x*)/cos(alpha). Если же эта клетка пуста, то проверяем следующие точки: Xi+1=Xi+h, Yi+1=Yi+htan(alpha). Здесь i-ая точка соответствует клетке (i*+i,[Yi/h]). Проверка происходит до тех пор, пока мы либо не наткнемся на занятую клетку, либо не выйдем за пределы лабиринта.

Теперь рассмотрим случай, когда cos(alpha)<0 (alpha то pi/2 до 3pi/2). Ближайшая точка пересечения луча с линией вида x=ih описывается формулами: x1=i*h, y1=y*-(x*- 1)tan(alpha)=y*+(x1-x*)tan(alpha). Первой проверяется клетка (i*-1,[y1/h]). Если она занята, то пересечение найдено и расстояние до точки пересечения равно d=(x1-x*)/cos(alpha). Иначе необходимо проверить остальные точки пересечения: Xi+1=Xi-h, Yi+1=Yi-htan(alpha). Для точки (Xi,Yi) следует проверить клетку (i*-i,[Yi/h]). Если она занята, то расстояние до точки пересечения составит d=(Xi-x*)/cos(alpha).

       Получаем следующий код. 

float        checkHWalls ( float angle )

{

        int        xTile = (int) locX;

        int        yTile = (int) locY;

        float        xIntercept;

        float        yIntercept;

        float        xStep;

        float        yStep;

        int        dyTile;

        if (fabs ( sin ( angle ) ) < 1e-7 )

                return 10000.0;

        if ( angle <= ANGLE_180 )

        {

                yTile ++;

                xStep = 1 / tan ( angle );

                yStep = 1;

                yIntercept = yTile;

                dyTile = 1;

        }

        else

        {

                yTile --;

                yStep = -1;

                xStep = -1 / tan ( angle );

                yIntercept = yTile + 1;

                dyTile = -1;

        }

        xIntercept = locX + (yIntercept - locY) / tan ( angle );

        for ( ; ; )

        {

                xTile = xIntercept;

                if ( xTile < 0 || xTile > 52 || yTile < 0 || yTile > 9 )

                        return 10000.0;

                if ( worldMap [yTile][xTile] != ' ' )

                        return ( yIntercept - locY ) / sin ( angle );

                xIntercept += xStep;

                yIntercept += yStep;

                yTile      += dyTile;

        }

}

void        drawView ()

{

        float        phi;

        float        distance;

        totalFrames++;

        for ( int col = 0; col < 320; col++ )

        {

                phi = angle + rayAngle [col];

                if ( phi < 0 )

                        phi += 2 * M_PI;

                else

                if ( phi >= 2 * M_PI )

                        phi -= 2 * M_PI;

                float        d1 = checkVWalls ( phi );

                float        d2 = checkHWalls ( phi );

                distance = d1;

                if ( d2 < distance )

                        distance = d2;

                distance *= cos ( phi - angle );        //adjustment for fish-eye

                drawSpan ( distance, WALL_COLOR, col );

        }

}

Для задания углов лучей здесь используется массив rayAngle - для каждого луча указан угол между направлением луча и направлением взгляда игрока. Наиболее простым способом описания этого массива является задание углов с постоянным шагом, но, т.к. этот способ вызывает некоторые искажения, применим следующий алгоритм: